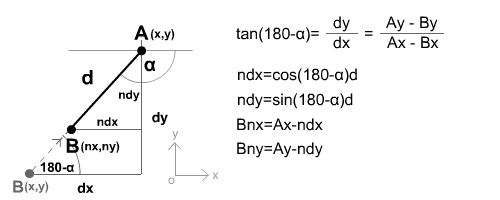Advanced inverse kinematics

The inverse kinematics system is a point-based system, in which members take effect on each other according to a few formulas:

- Points have to keep their distance from each other
- Desired points have to preserve their angle or limiting angle from other desired points

Part 1 - Keeping distance

We have points A and B, the required distance between them is d. What happens if one of them moves farther?

Fig 1

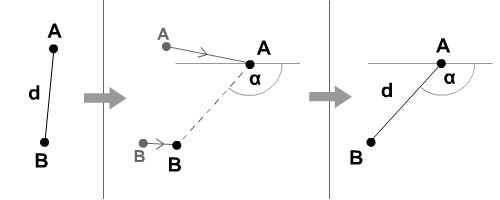
Our task is simple in this case. If A moves farther, we can determine the directional angle of the two points, and we have to make the distance constant again.

Fig 2

We know every coordinate, so we can determine x and y distances, and with the use of tangent we can get the desired angle between A and B, finally we can calculate the new coordinates. Fig 2 is defined in a normal positioned coordinate system (in the first quarter of the cartesian system), don't forget about flash flipping the y axis, and the upper left corner is the origin.

It looks much more simple in actionscript, because we can use the fantastic Math.atan2 function, where only dy and dx distances are required, and its returning interval is between -¶ and +¶. But be careful: the angles are also flipped because of the flipped y-axis !

//calculating the angle
var dx=pt_B._x-pt_A._x;
var dy=pt_B._y-pt_A._y;
var alpha=Math.atan2(dy,dx); 


//setting new position
var d=50;
pt_B._x=pt_A._x+Math.cos(alpha)*d;
pt_B._y=pt_A._y+Math.sin(alpha)*d;
				

To make things more spectacular, we should try to make an IK chain at this point. The easiest way to implement it is a recursive moving function.

move = function (parent) 
{
	makemove(this,parent);
	
	//this.nb = neighbours of the actual member
	for (var a=0;a < this.nb.length;++a) {
		if (parent!=this.nb[a]) this.nb[a].move(this);
	}
};

makemove = function(child,parent) 
{
	var dx = child._x-parent._x;
	var dy = child._y-parent._y;
	var alpha = Math.atan2(dy, dx);
	child._x = parent._x+Math.cos(alpha)*d;
	child._y = parent._y+Math.sin(alpha)*d;
	child._rotation=(Math.PI+alpha)*180/Math.PI;
} 
				

We store the neighbours in an array, so that a member can have an arbitrary number of neighbours, but there must not be a circle in the chain, because it results in a neverending loop.

Part 2 - Preserving angle

We have a quite nice chain now, but it is a little bit awkward. Let's see how we should maintain a constant angle relative to a third point.

Fig 3

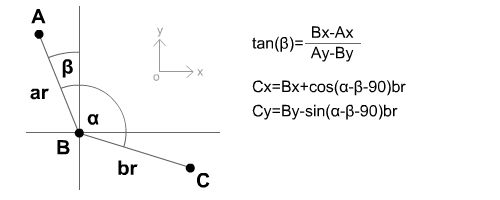
It's quite clear that we first have to determine the angle between the two parent-points (A and B), and with the constant opening-angle (alpha) we can calculate the position of the third point. (It is much more simple in actionscript because of Math.atan2). But our code should be more complicated because we want to configure each member separately, therefore, defining an IKMember class is necessary. We also have to define the SetAngles function, which calculates the angles of the fixed angled neighbours.

IKMember.prototype.SetAngles = function(parent) 
{
	var a,b,angle;
	
	//this.fpr = fixed angled pair
	
	if (this.fpr!=undefined) 
	{
		var node = this.fpr;
		if (node[1] == parent) 
		{
			//have to move first neighbour
			a = node[1];
			b = node[0];
			angle = 2*Math.PI-node[2]; //have to switch direction
		} else {
			//have to move second neighbour
			a = node[0];
			b = node[1];
			angle = node[2];
		} 
		
		var ax = a._x-this._x;
		var ay = a._y-this._y;
		var aangle = Math.atan2(ay, ax);
		b._x = this._x+Math.cos(aangle+angle)*d;
		b._y = this._y+Math.sin(aangle+angle)*d;
	}
};

The result:

art 3 - Maintaining limiting angles and making the junction point relative

Here comes the most difficult and most spectacular part: we have to restrict the movement interval of the points between limiting angles. We have to check, that the points fixated in Part 1 are within, above or under the limiting interval, if they aren`t within, we have to reposition them to the closest limit.

Fig 4

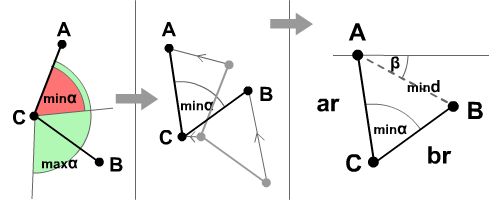
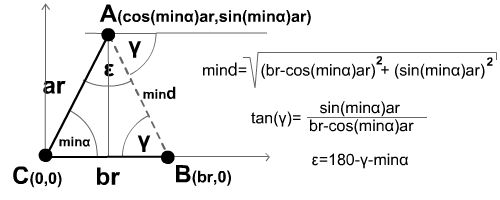
If B moves farther, the other two points have to move as well, preserving the minimal limiting angle alpha. To achieve this, we have to calculate betha between A and B, and the minimal distance mind, what minalpha can permit.

The easiest way to calculate mind is to place the CAB triangle in the origin of a coordinate system, and with the help of ar, br, minalpha and Pythagoras we can calculate the missing data.

Fig 5

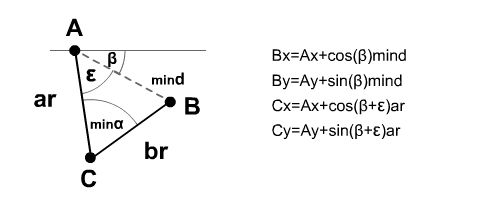
If we have mind and epsylon, we also have the position of the other two points as shown in fig 6.

Fig 6

To achieve this in flash we have to further improve our source.

IKMember.prototype.SetAngles = function(parent)
{
	var a,b,c,sangle;
	
	if (this.fpr!=undefined) 
	{
		var border=0;
		var node = this.fpr;
		if (node[1] == parent) 
		{	
			//have to move first neighbour and itself
			a = node[1];
			b = node[0];
			c = this;
			sangle = 2*Math.PI-node[2]-node[3];
		} else if (node[0] == parent) {
			//have to move second neighbour and itslef
			a = node[0];
			b = node[1];
			c = this;
			sangle = node[2];
		} else {
			//if parent is not a fixed member, have to move just second neighbour
			a = node[0];
			b = node[1];
			c = "";
			sangle = node[2];
		}
	
		var ax = a._x-this._x;
		var ay = a._y-this._y;
		var aangle = Math.atan2(ay, ax);
		var bx = b._x-this._x;
		var by = b._y-this._y;
		var bangle = Math.atan2(by, bx);
		maxangle = node[3];
		
		if (maxangle == 0) 
		{
			//if theres no limiting angle,
			//just places member to its position definied by the angle
			b._x = this._x+Math.cos(aangle+sangle)*d;
			b._y = this._y+Math.sin(aangle+sangle)*d;
		} else {
			//must not to go under 0
			if (bangle < aangle) bangle += 2*Math.PI; 
			
			//if there is a limiting angle(sangle and sangle+maxangle) 
			//checks if present position is 
			//under or over the limit, and sets closest border.
			//if its under the lowest limit
			if (bangle < aangle+sangle) border = sangle;
			
			//if its over the highest limit
			if (bangle>aangle+sangle+maxangle) border = sangle+maxangle;
			
			if (border != 0) 
			{
				var cx = b._x-a._x;
				var cy = b._y-a._y;
				var cangle = Math.atan2(cy, cx);
				
				//calculates the ar and br sided (d and d here), 
				//limiting angled triangle described in fig 5
				var px = d-Math.cos(border)*d;
				var py = Math.sin(border)*d;
				var mind = Math.sqrt(px*px+py*py);
				var gamma = Math.atan2(py, px);
				var deltha = Math.PI-border-gamma;
				
				//the third angle of the triangle, at origo
				//and repositioning
				b._x = a._x+Math.cos(cangle)*mind;
				b._y = a._y+Math.sin(cangle)*mind;
				
				var thisang = cangle+deltha;
				c._x = a._x+Math.cos(thisang)*d;
				c._y = a._y+Math.sin(thisang)*d;
			}
		}
	}
};

As you see, i made a little craft here: we have to observe which neighbour calls our member, for if we adjusted the members to the junction point, it would be unnatural; imagine people walking with a static knee, with only the ankle and the haunch moving.

I configured something skeleton-like to close the tutorial.

If you want to know more about the algorithm, check my IKGround prototype.

I hope my first tutorial was useful. Don't let the pay-sites gag you, don't forget what Plato said: wisdom can't and mustn't be sold for money. I also encourage you to send tutorials if you can. Oh, and also don't forget what Bill Gates said: 640K should be enough for everything, so code everything you can, and don't go over 640Kbit/8/1024=78,125 Kbyte!!! :)